#OI #算法 #数据结构 #Treap

Treap 笔记

By Zirnc

February 09, 2022

5 minutes

Treap = Tree + Heap

二叉搜索树（BST）

在学习 Treap 之前，需要先了解一下二叉搜索树（BST, Binary Search Tree）：

设 $x$ 是二叉搜索树中的一个结点。如果 $y$ 是 $x$ 左子树中的一个结点，那么 $y.key \lt x.key$。如果 $y$ 是 $x$ 右子树中的一个结点，那么 $y.key \gt x.key$。
BST 上的基本操作所花费的时间与这棵树的高度成正比。对于一个有 $n$ 个结点的二叉搜索树中，这些操作的最优时间复杂度为 $O(\log n)$，最坏为 $O(n)$。随机构造这样一棵二叉搜索树的期望高度为 $O(\log n)$。然而，当这棵树退化成链时，则同样的操作就要花费 $O(n)$ 的最坏运行时间。

由于普通 BST 容易退化，对于它的实现就不再赘述。在实践中需要使用如 Treap 这样的平衡二叉搜索树。

Treap

顾名思义，Treap 是树和堆的结合。它的数据结构既是一个二叉搜索树，又是一个二叉堆。

在 Treap 的每个结点中，除了 $key$ 值，还要保存一个 $fix$（更常见的是 $priority$）值。这个值是随机值，以它为依据来同时建立最大堆（或最小堆）。因为 $fix$ 值是随机的，所以可以让这棵树更加平衡，高度更接近 $O(\log n)$。它的各种操作期望时间复杂度都是 $O(\log n)$。

旋转式 Treap

旋转式 Treap 的常数较小。

旋转

左旋/右旋操作不会破坏 BST 的性质，并可以通过它来维护堆，使树平衡。

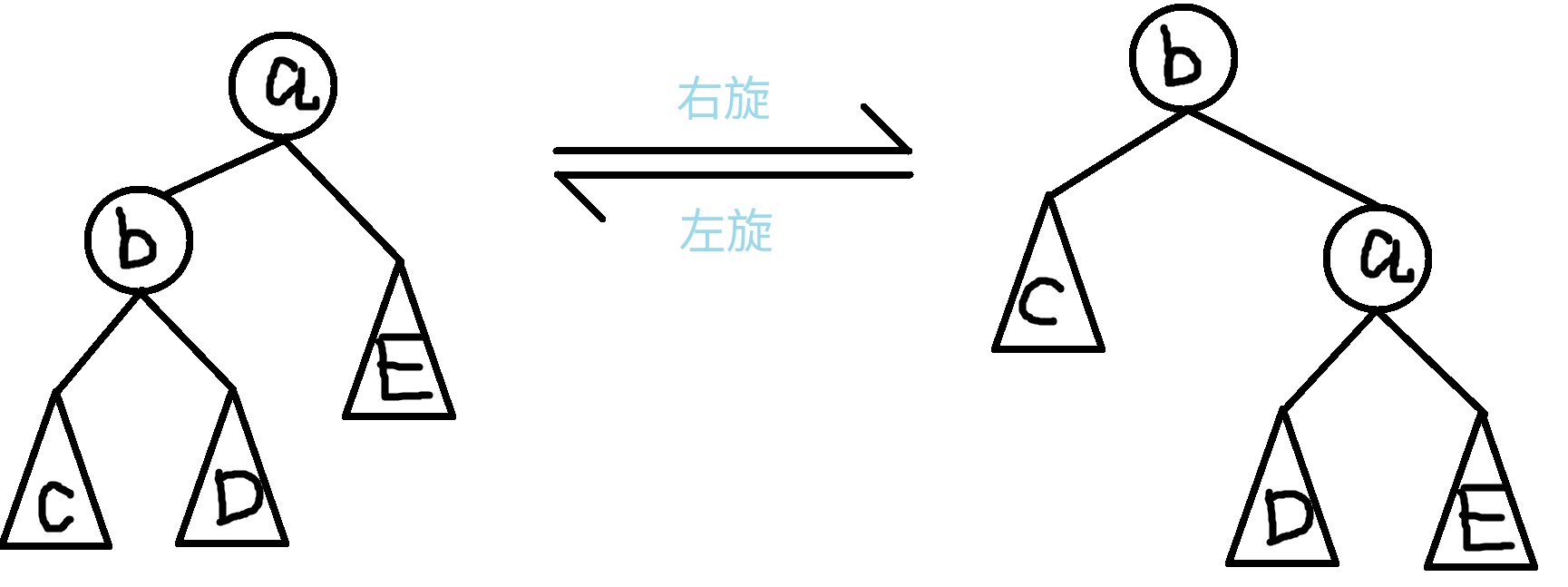
如图，以右旋为例。假设现在左边树 $b$ 的 $fix$ 值大于 $a$ 的 $fix$ 值，然而 $b$ 是 $a$ 的儿子，那么就不符合最大堆的性质，需要进行右旋，变成了右边的树。

但是为什么在旋转的过程中没有破坏 BST 的性质呢？设 $c \in C, d \in D, e \in E$。由左树知 $c \lt b \lt d \lt a \lt e$。再由旋转之后树的结构可以得出 $c \lt b \lt d \lt a \lt e$，这两个式子是一样的。所以，这棵树依然是 BST。

在插入和删除操作中都要按需进行旋转操作。

插入

根据 BST 的性质，找到相应的位置创建新叶子结点就可以了。如果不符合最大堆性质，进行旋转操作。

删除

删除一个元素时，可以对被删除的结点分类讨论：

没有子结点：直接就成空的了
只有一个子结点：把被删除结点设成它仅有的儿子即可
有两个子结点：选出两个儿子中 $fix$ 值较大的一个，通过旋转操作把它设成新的根，这样要删除的结点就只有一个儿子了，按照情况 2 处理。这种方法保证满足了 BST 和最大堆的性质。

在程序实现时，实际上情况 1 和 2 的代码是一样的，所以只用分两类。

以 P3369 【模板】普通平衡树 - 洛谷为例，代码如下。

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
#include <algorithm>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <vector>

using namespace std;
const int INF = 1000000009;
struct NODE {
  int val, fix, size; // size 指树的总结点数
  NODE *left, *right;
  NODE(const int val) : val(val) {
    fix = rand();
    left = right = NULL;
    size = 1;
  }
};
void maintain(NODE *&p) {
  p->size = 1;
  if (p->left != NULL)
    p->size += p->left->size;
  if (p->right != NULL)
    p->size += p->right->size;
}
void rightRotate(NODE *&p) {
  NODE *tmp = p->left;
  p->left = tmp->right;
  tmp->right = p;
  p = tmp;
  maintain(tmp->right);
  maintain(tmp);
}
void leftRotate(NODE *&p) {
  NODE *tmp = p->right;
  p->right = tmp->left;
  tmp->left = p;
  p = tmp;
  maintain(tmp->left);
  maintain(tmp);
}
void insert(NODE *&p, const int value) {
  if (p == NULL) {
    p = new NODE(value);
  } else if (value <= p->val) {
    insert(p->left, value);
    if (p->left->fix < p->fix)
      rightRotate(p);
  } else {
    insert(p->right, value);
    if (p->right->fix < p->fix)
      leftRotate(p);
  }
  maintain(p);
}
int count(const NODE *p, const int value) {
  if (!p)
    return 0;
  if (p->val == value)
    return 1;
  if (value <= p->val)
    return count(p->left, value);
  return count(p->right, value);
}
void remove(NODE *&p, const int value) {
  if (!p)
    return;
  if (p->val == value) {
    if (p->left == NULL || p->right == NULL) {
      NODE *tmp = p;
      if (p->right)
        p = p->right;
      else
        p = p->left;
      delete tmp;
    } else if (p->left->fix < p->right->fix) {
      rightRotate(p);
      remove(p->right, value);
      maintain(p);
    } else {
      leftRotate(p);
      remove(p->left, value);
      maintain(p);
    }
  } else if (value < p->val) {
    remove(p->left, value);
    maintain(p);
  } else {
    remove(p->right, value);
    maintain(p);
  }
}
int getrank(const NODE *p, int value) {
  if (!p)
    return INF;
  int leftsize = 0;
  if (p->left != NULL)
    leftsize = p->left->size;
  if (p->val == value)
    return min(leftsize + 1, getrank(p->left, value));
  else if (value < p->val)
    return getrank(p->left, value);
  else if (value > p->val)
    return leftsize + 1 + getrank(p->right, value);
}
int find(const NODE *p, int rank) {
  if (!p)
    return 0;
  int leftsize = 0;
  if (p->left != NULL)
    leftsize = p->left->size;
  if (leftsize >= rank)
    return find(p->left, rank);
  else if (leftsize + 1 == rank)
    return p->val;
  else
    return find(p->right, rank - leftsize - 1);
}
int getpre(const NODE *p, int value) { // 前驱
  if (!p)
    return -INF;
  if (p->val >= value)
    return getpre(p->left, value);
  else
    return max(p->val, getpre(p->right, value));
}
int getnext(const NODE *p, int value) { // 后继
  if (!p)
    return INF;
  if (p->val <= value)
    return getnext(p->right, value);
  else
    return min(p->val, getnext(p->left, value));
}
int n;
NODE *root;
int main() {
  scanf("%d", &n);
  while (n-- > 0) {
    int opt, x;
    scanf("%d %d", &opt, &x);
    if (opt == 1) {
      insert(root, x);
    } else if (opt == 2) {
      remove(root, x);
    } else if (opt == 3) {
      printf("%d\n", getrank(root, x));
    } else if (opt == 4) {
      printf("%d\n", find(root, x));
    } else if (opt == 5) {
      printf("%d\n", getpre(root, x));
    } else if (opt == 6) {
      printf("%d\n", getnext(root, x));
    }
  }
  return 0;
}

无旋 Treap

无旋 Treap 的核心操作是分裂、合并。

分裂（Split）

分裂操作会将原 Treap 一分为二，第一个 Treap 中的结点关键值都小于等于 $key$，第二个中都大于 $key$。使用递归实现。

若当前关键值大于 $key$，那么当前结点连同右子树都属于第二个 Treap，继续往左子树递归。

若当前关键值小于等于 $key$，那当前结点连同左子树都属于第一个 Treap。继续往右子树递归。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
pair<NODE *, NODE *> split(NODE *u, const int value) {
  if (u == nullptr)
    return make_pair(nullptr, nullptr);
  if (u->value > value) {
    auto tmp = split(u->ch[0], value);
    u->ch[0] = tmp.second;
    maintain(u);
    return make_pair(tmp.first, u);
  } else {
    auto tmp = split(u->ch[1], value);
    u->ch[1] = tmp.first;
    maintain(u);
    return make_pair(u, tmp.second);
  }
}

合并（Merge）

合并函数接受两棵树，其中第一棵的值都小于第二棵。每一次根据两棵树的根的 $fix$ 值来确定新树的根，然后递归合并子树。

当两棵树任何一个为空时，返回另一个。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
NODE *merge(NODE *l, NODE *r) {
  if (l == nullptr)
    return r;
  if (r == nullptr)
    return l;
  if (l->fix < r->fix) {
    l->ch[1] = merge(l->ch[1], r);
    maintain(l);
    return l;
  } // else
  r->ch[0] = merge(l, r->ch[0]);
  maintain(r);
  return r;
}

插入

将树分裂成两个部分：$A=\lbrace x \mid x \le key \rbrace$、$B= \lbrace x \mid x \gt key \rbrace$，先将要插入的值合并入 $A$，最后合并 $A$ 和 $B$。

1
2
3
4
5
void insert(int value) {
  auto tmp = split(root, value);
  tmp.first = merge(tmp.first, new NODE(value));
  root = merge(tmp.first, tmp.second);
}

删除

将树分裂成三个部分：$A= \lbrace x \mid x \lt key \rbrace$、$B= \lbrace x \mid x = key \rbrace$、$C= \lbrace x \mid x \gt key \rbrace$，然后合并 $A$ 和 $C$。

1
2
3
4
5
6
void erase(int value) {
  auto tmp = split(root, value - 1);
  auto tmp2 = split(tmp.second, value);
  delete tmp2.first;
  root = merge(tmp.first, tmp2.second);
}

致谢：

YWQ (Monad)
OI Wiki CC BY-SA 4.0
《算法导论》
Algorithms for Competitive Programming CC BY-SA 4.0
Treap - Wikipedia CC BY-SA 3.0

告别 2021

关于 int 与 long long 的运算速度