线段树是一种高端的数据结构,可以用来在区间上进行信息统计。它能够在 $O(logN)$ 的时间复杂度内实现单点/区间修改、区间找最大值/最小值/总和/…,适用于大规模的区间统计。
如下图就是一棵线段树。在结点中,你可以存对应区间的最大值,最小值,总和等等。

对于每一个结点 $i$,它的两个子结点分别是 $2i$ 和 $2i+1$。因此,在开树的数组时,最好要开到 $4N$ 的大小。
关于 $4N$,详见 OI-Wiki。
建树
下面是一个求区间和的线段树的建树代码。
通过 DFS 建树,到叶结点,然后一路回溯求出和。
1
2
3
4
5
6
7
8
9
10
11
12
13
| void build_tree(int cur, int left, int right) {
// cur 为当前树的根,[left, right] 是当前树对应的区间
if (left == right) {
// 到叶子节点了,区间长度为 1,总和就是它本身
tree[cur] = a[left];
return ;
}
int leftSon = cur*2, rightSon = leftSon+1;
int mid = (left+right)/2;
build_tree(leftSon, left, mid);
build_tree(rightSon, mid+1, right);
tree[cur] = tree[leftSon]+tree[rightSon]; // 求和
}
|
这里求 leftSon,rightSon,mid 的模式在线段树的所有操作中都会用到。
区间查询
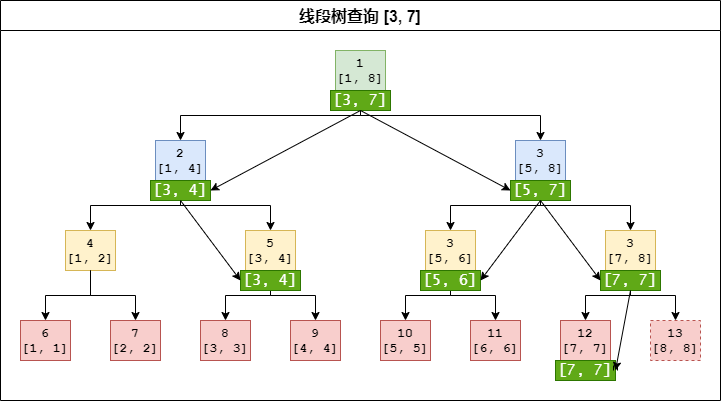
对于一个不恰好的区间,我们可以不断地把它拆分成两个恰好的区间再进行合并。
如图所示,拆分过程如下:
- [3, 7]
- [3, 4], [5, 7]
- [3, 4], [5, 6], [7, 7]
在实际 DFS 过程中,我们可以分为三种情况:
- 当前结点对应区间和要查询的区间完全无关,直接退出
- 当前结点对应区间完全处于要查询的区间范围,返回当前结点的值
- 两个区间部分相交,继续拆分为 1 或 2 情况
1
2
3
4
5
6
7
8
9
| long long query(int cur, int l, int r, int x, int y) {
// cur 为当前树的根,[l, r] 是当前树对应的区间,[x, y] 是要查询的区间
if (y < l || r < x) return 0; // 1. 相离
if (x <= l && r <= y) return tree[cur]; // 2. 完全包含
// 3. 相交
int leftSon = cur*2, rightSon = leftSon+1;
int mid = (l+r)/2;
return query(leftSon, l, mid, x, y) + query(rightSon, mid+1, r, x, y); // 求和
}
|
区间修改
单点修改并没有什么意思,就不讲了。
区间修改当然不是重复做单点修改,否则使用线段树就很没有必要了。为了避免走到底下去,我们要使用一个懒惰标记(lazy tag)。当一个大区间内所有的小单位都要进行同样的修改操作时,只需要在大区间做一次标记就可以了。到了必须要走下去(即查询更小的区间或修改更小的区间)的时候,再把懒惰标记下放。
下面以一个区间增加一个值并进行区间查询为例。
首先定义一个结构体,其中 add 就是记录这个区间需要增加的值。
1
2
3
4
| struct node
{
long long sum, add;
} tree[4 * MAXN];
|
下放操作:
1
2
3
4
5
6
7
8
9
10
11
12
13
| void pushdown(int cur, int left, int mid, int right)
{
// 将当前结点的 add 值下放给子结点
const int leftSon = cur * 2, rightSon = leftSon + 1;
// 更新总和(区间元素个数*每个元素要增加的值)
tree[leftSon].sum += (mid - left + 1) * tree[cur].add;
tree[rightSon].sum += (right - mid) * tree[cur].add;
// 更新 add 值
tree[leftSon].add += tree[cur].add;
tree[rightSon].add += tree[cur].add;
// 当前结点的懒惰标记已经下放,需要清零
tree[cur].add = 0;
}
|
区间增加一个值:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| void update(int cur, int left, int right, int x, int y, ll c)
{
if (left > y || right < x) // 相离
return;
if (left >= x && right <= y) // 完全包含
{
// 给当前区间整体增加 c
tree[cur].sum += (right - left + 1) * c;
// 打标记
tree[cur].add += c;
// 这时不需要子结点的值,所以不必下放
return;
}
// 相交
// 分成两个子区间,必须要往下走了
int mid = (left + right) / 2;
int leftSon = cur * 2, rightSon = leftSon + 1;
pushdown(cur, left, mid, right); // 先下放标记
update(leftSon, left, mid, x, y, c);
update(rightSon, mid + 1, right, x, y, c);
tree[cur].sum = tree[2 * cur].sum + tree[2 * cur + 1].sum; // 最后汇总总和
}
|
区间查询:
1
2
3
4
5
6
7
8
9
10
11
12
13
| ll query(int cur, int left, int right, int x, int y)
{
if (left > y || right < x) // 相离
return 0;
if (left >= x && right <= y) // 完全包含
return tree[cur].sum;
// 相交
// 拆成两个字区间再求和
int mid = (left + right) / 2;
int leftSon = cur * 2, rightSon = leftSon + 1;
pushdown(cur, left, mid, right); // 必须往下走,下放标记
return query(leftSon, left, mid, x, y) + query(rightSon, mid + 1, right, x, y);
}
|
通过上面的代码,我们可以看到:懒惰标记就是为了不往下走,尽量在更大的区间做一次操作。必要时才往下下放标记。它不会主动做事,而是到你需要的时候才花时间去做。通过这样节省了很多时间。
小结
总的来说,线段树不是一个很难的数据结构,但是很实用。
感谢 lgj 老师!

