动态开点线段树
常规写法的线段树只能维护不算很长的数组,由于空间不够,对于 $10^9$ 级别的数组却不能很好地维护。所以,我们要用到动态开点线段树。
核心思想:节点只有在有需要的时候才被创建。
比如说,要求在一个长度为 $n < 10^9$ 的数组上实现区间求和、单点修改的操作,初始数组元素值均为 0。
那么,我们一开始只创建一个根结点,接下来遵循动态开点的核心思想进行操作。
比如下面这张图的例子,我们依次修改 1, 2, 8 三个结点,途中创建了必要的结点。而在图中没有显示的空结点并没有被创建,视为 0,这样就节省了空间。
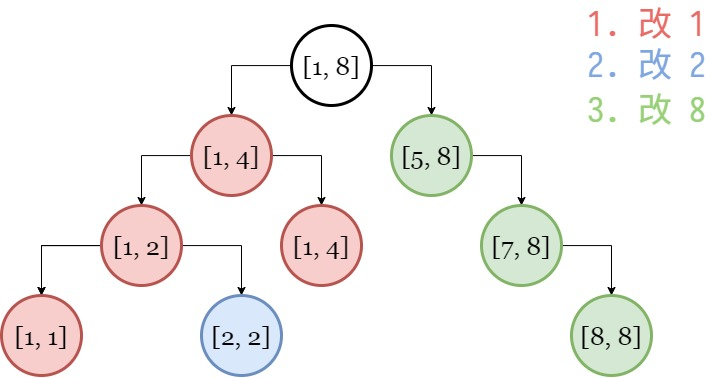
那么对于区间修改时,会有 pushdown() 操作,可能会修改一个不存在的结点。这时有两个解决方案:
- 在
pushdown() 时,如果缺少孩子,就直接创建一个新的孩子就可以了。 - 使用 标记永久化 技巧(李超线段树),让结点不再进行
pushdown(),进一步节省了空间。
复杂度分析:单次操作的时间复杂度是不变的,为 $O(\log n)$。对于空间复杂度,由于每次操作都有可能创建并访问全新的一系列结点,因此 $m$ 次操作的空间复杂度是 $O(m\log n)$,不再是原本线段树的 $O(n)$。
代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| int n, cnt, root; // cnt 表示当前结点个数
int sum[N*2], ls[N*2], rs[N*2];
void upd(int& rt, int l, int r, int p, int f) { // 注意这里传入一个引用,可以修改 ls 或 rs 数组
if (!rt) rt = ++cnt; // 当结点为空时,创建一个新的结点
if (l == r) {
sum[rt] += f;
return;
}
int m = (l + r) >> 1;
if (p <= m)
upd(ls[rt], l, m, p, f);
else
upd(rs[rt], m + 1, r, p, f);
sum[rt] = sum[ls[rt]] + sum[rs[rt]]; // pushup
}
int query(int rt, int l, int r, int L, int R) {
if (!rt) return 0; // 如果结点为空,返回 0
if (l >= L && r <= R) return sum[rt];
int m = (l + r) >> 1, ans = 0;
if (L <= m)
ans += query(ls[rt], l, m, L, R);
if (R > m)
ans += query(rs[rt], m + 1, r, L, R);
return ans;
}
|
可持久化线段树
可持久化线段树,就是可以存储历史信息的线段树。
比如我们对数组进行了 n 次修改,然后突然希望回到第 i 个版本,然后又基于这个版本进行一些新的修改等,就是可持久化线段树需要解决的问题。
最暴力的想法是,对于每一次修改,都重新建一棵完整的线段树。然后,空间爆炸了。
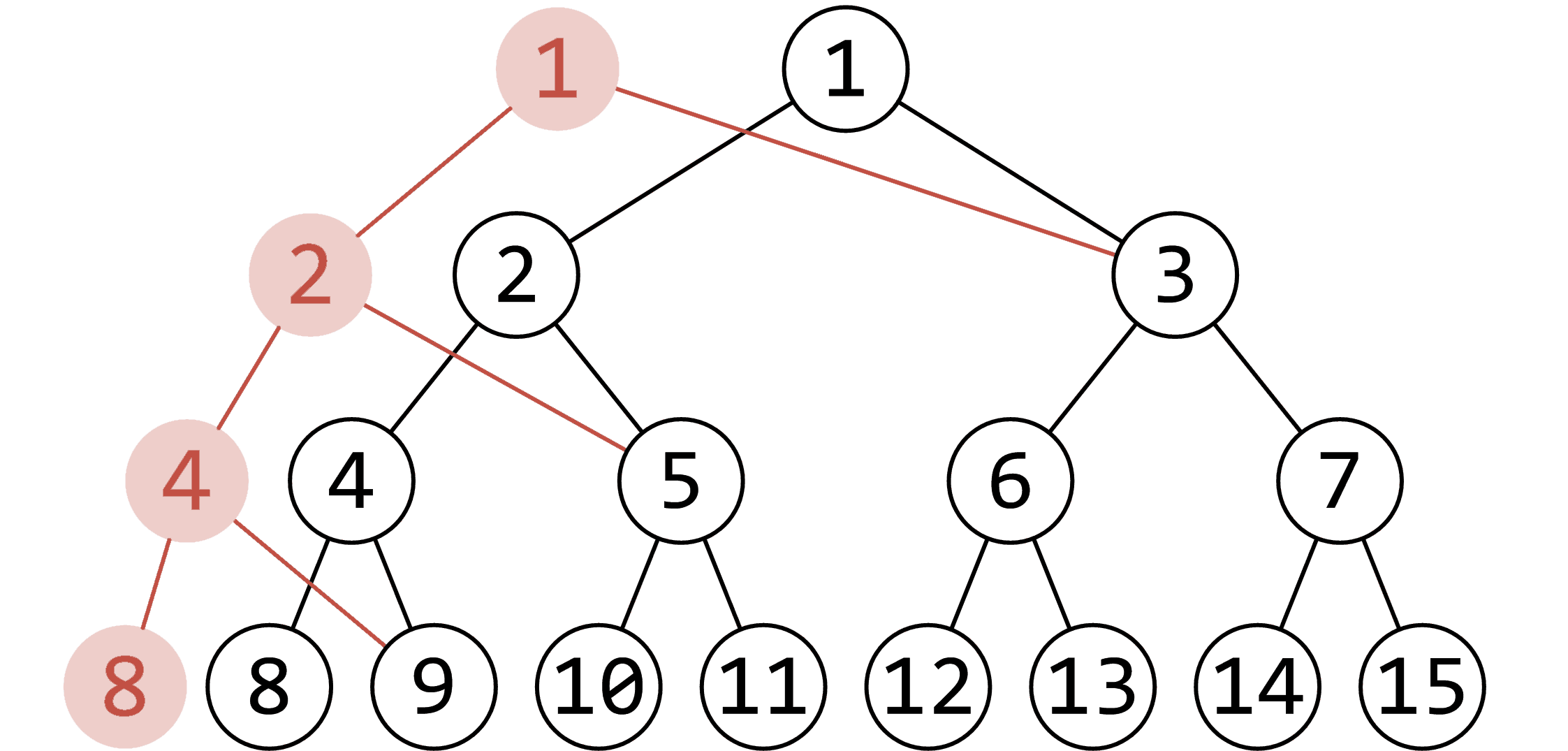
我们分析一下,就会发现每一次修改时,改变的结点的个数都是线段树的深度 $\log n$。如图,我们修改了结点 $8$ 的值,受到影响的结点都在从根结点 $1$ 到 $8$ 的路径上,即 $1, 2, 4, 8$。其他的结点都是不变的。因此,我们只需要重新创建有改动的结点即可,例如 $1(new), 2(new), 4(new), 8(new)$(新的结点是动态开点的,编号和原来的不一样,因此这里用 $(new)$ 标注)。然后,例如对于新的根结点 $1(new)$,将左儿子指向新的 $2(new)$,右儿子和旧的根结点 $1(old)$ 的右儿子相同,是 $3(old)$,不用修改。
例题
Luogu-P3919 【模板】可持久化线段树 1(可持久化数组)
如题,你需要维护这样的一个长度为 $ N $ 的数组,支持如下几种操作
- 在某个历史版本上修改某一个位置上的值
- 访问某个历史版本上的某一位置的值
此外,每进行一次操作(对于操作2,即为生成一个完全一样的版本,不作任何改动),就会生成一个新的版本。版本编号即为当前操作的编号(从1开始编号,版本0表示初始状态数组)
$ 1 \leq N, M \leq {10}^6, 1 \leq {loc}_i \leq N, 0 \leq v_i < i, -{10}^9 \leq a_i, {value}_i \leq {10}^9$
程序实现:
为了保险,线段树数组的大小应设为 n << 5。洛谷上关于此的讨论。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
| #include <bits/stdc++.h>
using namespace std;
const int MAXN = 1000006;
int n, m;
int a[MAXN];
int rt[MAXN << 5], lc[MAXN << 5], rc[MAXN << 5], sm[MAXN << 5], ver = 0, tot = 0;
void build(int& rt, int l, int r) {
rt = ++tot;
if (l == r) {
sm[rt] = a[l];
return;
}
int m = (l + r) >> 1;
build(lc[rt], l, m);
build(rc[rt], m + 1, r);
}
void update(int& rt, int pre, int l, int r, int q, int v) { // pre:原结点
rt = ++tot;
lc[rt] = lc[pre];
rc[rt] = rc[pre];
sm[rt] = sm[pre]; // 复制原结点的信息,之后按需修改
if (l == r) {
sm[rt] = v;
return;
}
int m = (l + r) >> 1;
if (q <= m)
update(lc[rt], lc[pre], l, m, q, v); // 新建左子结点,但是右子结点不变
else
update(rc[rt], rc[pre], m + 1, r, q, v); // 反之
}
int query(int rt, int l, int r, int q) {
if (l == r) return sm[rt];
int m = (l + r) >> 1;
if (q <= m) return query(lc[rt], l, m, q);
return query(rc[rt], m + 1, r, q);
}
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> a[i];
build(rt[0], 1, n);
while (m--) {
int v, opt, loc, val;
cin >> v >> opt >> loc;
if (opt == 1) {
cin >> val;
update(rt[++ver], rt[v], 1, n, loc, val); // rt[++ver] 以 rt[v] 为基础
} else {
cout << query(rt[v], 1, n, loc) << endl;
rt[++ver] = rt[v];
}
}
return 0;
}
|
权值线段树
普通的线段树维护的是区间内最值或总和,而权值线段树每个结点维护的是在一个区间内的数出现的次数。因此,可以把权值线段树看作一个桶。举个例子,如果 $tree[1]$ 对应的区间是 $[1, 8]$,那么它的值就是 $1, 2, \cdots, 7, 8$ 在原数组中出现的次数之和。
权值线段树中,采用元素到下标数组映射的方式进行插入。当数据离散程度较大的情况,空间的利用效率比较低,这时候可以搭配离散化技巧(下面有例子)。
一个常见的应用是把权值线段树用于处理区间第 $K$ 小/大问题。
例题:Luogu-P1138 第 k 小整数 RECORD
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
| #include <algorithm>
#include <cstdio>
#include <iostream>
using namespace std;
const int MAXN = 10005;
int n, k, a[MAXN];
int tree[MAXN << 1], lc[MAXN << 1], rc[MAXN << 1], root = 0, tot = 0;
// 对于权值线段树来说,build 函数是没有必要的,因为默认值为 0
// 只不过这里为了节省空间用了动态开点,才需要 build()
void build(int &rt, int l, int r) {
rt = ++tot;
if (l == r) return;
int m = (l + r) >> 1;
build(lc[rt], l, m);
build(rc[rt], m + 1, r);
}
void update(int rt, int l, int r, int q) {
if (l == r) {
tree[rt] = 1; // 出现了 1 次
return;
}
int m = (l + r) >> 1;
if (q <= m)
update(lc[rt], l, m, q);
else
update(rc[rt], m + 1, r, q);
tree[rt] = tree[lc[rt]] + tree[rc[rt]]; // 区间内数的数量
}
int kth(int rt, int l, int r, int k) {
if (l == r) return l;
int m = (l + r) >> 1;
if (k > tree[lc[rt]]) return kth(rc[rt], m + 1, r, k - tree[lc[rt]]); // 在右半区间内
return kth(lc[rt], l, m, k); // 在左半区间内
}
int main() {
cin >> n >> k;
build(root, 1, n);
for (int i = 1; i <= n; i++) cin >> a[i];
sort(a + 1, a + n + 1); // 离散化+去重
n = unique(a + 1, a + 1 + n) - a - 1; // 记得 -1
if (k > n) {
cout << "NO RESULT\n";
return 0;
}
for (int i = 1; i <= n; i++) { update(root, 1, n, i); } // 离散化后,插入下标
cout << a[kth(root, 1, n, k)] << endl; // 离散化后,kth() 查到的是第 k 小整数的 **下标**
return 0;
}
|
注意:离散化时用 unique() 最后面一定要 -1!!!
可持久化权值线段树(主席树)
主席树名称来源于其发明人黄嘉泰的姓名的首字母缩写 HJT。
例题
Luogu-P3834 【模板】可持久化线段树 2
如题,给定 $n$ 个整数构成的序列 $a$,将对于指定的闭区间 $[l, r]$ 查询其区间内的第 $k$ 小值。
$1 \leq n,m \leq 2\times 10^5$,$|a_i| \leq 10^9$,$1 \leq l \leq r \leq n$,$1 \leq k \leq r - l + 1$。
首先看到第 $k$ 小问题,想到要使用权值线段树。
对于每一个数,我们都
我们先把问题简化一下:每次求 $[1, r]$ 区间内的 $k$ 小值。
这时,只要找到插入 $r$ 的版本的权值线段树,然后查找即可。
回到原问题:求 $[l, r]$ 区间内的 $k$ 小值。
我们发现,主席树其实具有前缀和的性质,查询 $[l, r]$ 可以转化为 $[1, r]$ 减去 $[1, l-1]$ 的对应区间的大小。
注意数据范围,$2\times 10^5$ 个数,$|a_i| \leq 10^9$,因此用离散化。
RECORD
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
| #include <bits/stdc++.h>
using namespace std;
const int MAXN = 200005;
int n, m, q;
int a[MAXN], b[MAXN];
int rt[MAXN << 5], lc[MAXN << 5], rc[MAXN << 5], sm[MAXN << 5], tot = 0;
void build(int& rt, int l, int r) {
rt = ++tot;
if (l == r) return;
int m = (l + r) >> 1;
build(lc[rt], l, m);
build(rc[rt], m + 1, r);
}
void update(int& rt, int pre, int l, int r, int q) {
rt = ++tot; // 动态开点
lc[rt] = lc[pre];
rc[rt] = rc[pre];
sm[rt] = sm[pre] + 1;
if (l == r) return;
int m = (l + r) >> 1;
if (q <= m)
update(lc[rt], lc[pre], l, m, q);
else
update(rc[rt], rc[pre], m + 1, r, q);
}
int query(int rt, int pre, int l, int r, int k) {
if (l == r) return l;
int x = sm[lc[rt]] - sm[lc[pre]]; // 对应区间相减
int m = (l + r) >> 1;
if (x >= k) return query(lc[rt], lc[pre], l, m, k);
return query(rc[rt], rc[pre], m + 1, r, k - x);
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
b[i] = a[i];
}
// 离散化
sort(b + 1, b + 1 + n);
q = unique(b + 1, b + 1 + n) - b - 1;
build(rt[0], 1, q);
for (int i = 1; i <= n; i++) {
int pos = lower_bound(b + 1, b + 1 + q, a[i]) - b;
update(rt[i], rt[i - 1], 1, q, pos);
}
while (m--) {
int l, r, k;
scanf("%d%d%d", &l, &r, &k);
printf("%d\n", b[query(rt[r], rt[l - 1], 1, q, k)]);
}
return 0;
}
|
参考资料

