Zirnc's Blog
关于 分类 友链 存档 标签

线段树之标记永久化

普通的线段树在做区间修改时依赖懒标记（lazy tag），当我们从一个点向下访问时，需要将标记 pushdown。能否避免如此多的 pushdown 操作呢？这时需要用到标记永久化技巧。

我们要做的就是将 lazy tag 永久地留在当前的结点，这时子树中的所有结点都不会被这个 tag 所影响。因此，子树中询问的最大值 = 实际最大值 - tag。当我们想得到正确答案时，只要将子树返回的最大值加上当前 tag 即可。

标记永久化存在局限性，需要满足不同的修改操作可以交换顺序，或者说对答案的贡献是独立的这一条件。

举个例子：区间设置+区间加法，先设置后加和先加后设置的结果是不一样的，因此不能交换顺序。如果使用标记永久化，就可能改变了这个顺序。

  1. 比如我们先设置后加，并且令设置的区间比加的区间大，因此加的 tag 在下方，设置的 tag 在上方。
  2. 根据前面的方法，我们会从下往上取 tag，也就是先加法，再设置。
  3. 这时我们发现，由于上层是一个设置操作，下面的所有答案最终都变成了设置的那个数字，下层操作就失效了。显然有问题。

总结：标记永久化就是不再下放标记，而是让标记永久地停留在当前结点上。在统计答案时再考虑标记的影响。

复杂度分析：由于标记不会下放，但如果有两个标记落在了一个结点上，我们不会分别存储这两个标记，而是加起来合成一个标记（$(+2) + (+3) = (+5)$）。因此，每个结点最多只有一个标记。询问时最多考虑 $\log n$ 个标记，复杂度和普通线段树相同 $O(\log n)$。

程序实现：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

int up(int p) { tree[p].mx = max(tree[p<<1].mx, tree[p<<1|1].mx)+tree[p].tag; }
int query(int p, int l, int r, int x, int y) {
  if (l >= x && r <= y) return tree[p].mx;
  int mid = (l + r) / 2, ans = -INF;
  if (x <= mid) ans = max(ans, query(p << 1, l, mid, x, y));
  if (y > mid) ans = max(ans, query(p << 1 | 1, mid + 1, r, x, y));
  return ans+tree[p].tag;
}
void update(int cur, int l, int r, int x, int y, int c) {
  if (l >= x && r <= y) {
    tree[cur].tag += c;
    tree[cur].mx += c;
    return;
  }
  int mid = (l + r) / 2;
  if (x <= mid) update(cur << 1, l, mid, x, y, c);
  if (y > mid) update(cur << 1 | 1, mid + 1, r, x, y, c);
  up(cur);
}

李超线段树

例题：Luogu-4097 [HEOI2013]Segment 要求在平面直角坐标系下维护两个操作（强制在线）：

  1. 在平面上加入一条线段。记第 $i$ 条被插入的线段的标号为 $i$，该线段的两个端点分别为 $(x_0,y_0)$，$(x_1,y_1)$。
  2. 给定一个数 $k$，询问与直线 $x = k$ 相交的线段中，交点纵坐标最大的线段的编号（若有多条线段与查询直线的交点纵坐标都是最大的，则输出编号最小的线段）。特别地，若不存在线段与给定直线相交，输出 $0$。

操作总数 $1 \leq n \leq 10^5$，$1 \leq k, x_0, x_1 \leq 39989$，$1 \leq y_0, y_1 \leq 10^9$。

将问题转化成以下的操作：

  • 加入一个一次函数，定义域为 $[l,r]$；
  • 给定 $k$，求定义域包含 $k$ 的所有一次函数中，在 $x=k$ 处取值最大的那个，如果有多个函数取值相同，选编号最小的。

注意：当线段垂直于 $y$ 轴时，如果按照一般的式子计算，会出现除以零的情况。假设线段两端点分别为 $(x,y_0)$ 和 $(x,y_1)$，$y_0<y_1$，则插入定义域为 $[x,x]$ 的一次函数 $f(x)=0\cdot x+y_1$。

首先，我们建立一棵线段树，每个结点代表一段 $x$ 轴上的区间，结点的懒标记表示一条线段，记为 $g$。

现在我们要插入线段 $f$。一直找到被 $f$ 完全覆盖的区间，进行分类讨论。

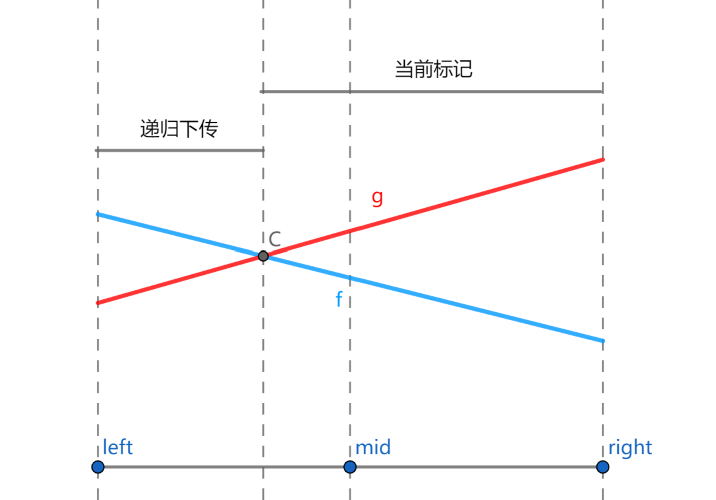
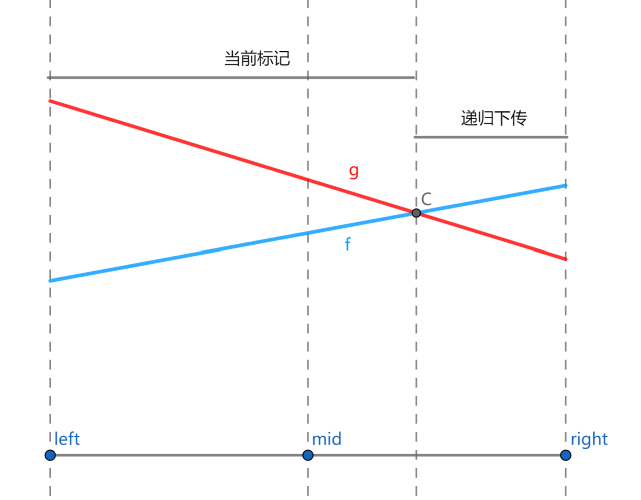
cross-l cross-r

如图，按新线段 $f$ 取值是否大于原标记 $g$，我们可以把当前区间分为两个子区间。其中 肯定有一个子区间被左区间或右区间完全包含，也就是说，在两条线段中，肯定有一条线段，只可能成为左区间的答案，或者只可能成为右区间的答案。我们用这条线段递归更新对应子树，用另一条线段作为懒标记更新整个区间，这就保证了递归下传的复杂度。当一条线段只可能成为左或右区间的答案时，才会被下传，所以不用担心漏掉某些线段。

具体来说，设当前区间的中点为 $mid$，我们拿新线段 $f$ 与原最优线段 $g$ 与 $x=mid$ 的交点的值作比较。

  1. 如果新线段 $f$ 更优，则将 $f$ 和 $g$ 交换。转化成了第 2 种情况。
  2. 对于中点处 $f$ 不如 $g$ 优的情况：
    • 若在左端点处 $f$ 更优，那么 $f$ 和 $g$ 必然在左半区间中产生了交点，$f$ 只有在左区间才可能优于 $g$，递归到左儿子中进行下传；
    • 若在右端点处 $f$ 更优，那么 $f$ 和 $g$ 必然在右半区间中产生了交点，$f$ 只有在右区间才可能优于 $g$，递归到右儿子中进行下传；
    • 若在左、右端点处 $g$ 都更优，那么 $f$ 不可能成为答案，不需要继续下传。

除了这两种情况之外，还有一种情况是 $f$ 和 $g$ 刚好交于中点，在程序实现时可以归入 $f$ 不如 $g$ 优的情况，结果会往 $f$ 更优的一个端点进行递归下传。

最后将 $g$ 作为当前区间的懒标记。

查询时，用到标记永久化。我们只需要找到所有覆盖了 $k$ 的区间，每次考虑这个标记对答案有怎样的贡献即可。

复杂度分析：查询的时间复杂度显然为 $O(\log n)$，而插入过程中，我们需要将原线段拆分到 $O(\log n)$ 个区间中，对于每个区间，我们又需要花费 $O(\log n)$ 的时间递归下传，从而插入过程的时间复杂度为 $O(\log^2 n)$。

RECORD

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112

#include <bits/stdc++.h>

using namespace std;
const int N = 1000005;
const int MOD1 = 39989;
const int MOD2 = 1000000000;
const double EPS = 1e-12;
struct line {
  double k, b;
  int l, r;
  int id;
} tree[N << 2];
int n;
double calc(line a, int x) {  // 计算纵坐标
  return x * a.k + a.b;
}
// 注意 cmp 写法。不要写成 a-b < EPS。
int cmp(double a, double b) {
  if (a - b > EPS) return 1;
  if (b - a > EPS) return -1;
  return 0;
}
void build(int rt, int l, int r) {
  tree[rt] = {0, 0, 1, 40000, 0};
  if (l == r) return;
  int m = (l + r) >> 1;
  build(rt << 1, l, m);
  build(rt << 1 | 1, m + 1, r);
}
void modify(int root, int l, int r, line k) { 
  if (l >= k.l && r <= k.r) { // 对线段完全覆盖到的区间进行修改
    // g: tree[root]; f: k.
    int m = (l + r) >> 1;
    if (cmp(calc(tree[root], m), calc(k, m)) == -1) swap(tree[root], k);

    int cl = cmp(calc(k, l), calc(tree[root], l)),
        cr = cmp(calc(k, r), calc(tree[root], r));
    // 3. 若在左右端点处 g 都更优，那么 f 不可能成为答案，不需要继续下传。
    if (cl == -1 && cr == -1) return;
    // 1. & 2. 注意题目要求下标尽量小，下标小的线段即使不更优，如果值相等，也可以下传。
    if (cl == 1 || (cl == 0 && k.id < tree[root].id)) modify(root << 1, l, m, k);
    if (cr == 1 || (cr == 0 && k.id < tree[root].id)) modify(root << 1 | 1, m + 1, r, k);
  } else {
    int m = (l + r) >> 1;
    if (k.l <= m) modify(root << 1, l, m, k);
    if (k.r > m) modify(root << 1 | 1, m + 1, r, k);
  }
}
pair<double, int> pmax(pair<double, int> x,
                       pair<double, int> y) {  // 注意题目要求下标尽量小
  if (cmp(x.first, y.first) == -1)
    return y;
  else if (cmp(x.first, y.first) == 1)
    return x;
  else
    return x.second < y.second ? x : y;
}

pair<double, int> query(int root, int l, int r, int x) {
  if (l == r) return {calc(tree[root], x), tree[root].id};

  int m = (l + r) >> 1;
  pair<double, int> ans = {calc(tree[root], x), tree[root].id};
  // 注意标记永久化，取 max 比较
  if (x <= m)
    ans = pmax(ans, query(root << 1, l, m, x));
  else
    ans = pmax(ans, query(root << 1 | 1, m + 1, r, x));
  return ans;
}
int main() {
  ios::sync_with_stdio(false);
  cin >> n;
  build(1, 1, 40000);
  int lastans = 0;
  int segi = 0;
  while (n--) {
    int op;
    cin >> op;
    if (op == 0) {
      int k;
      cin >> k;
      k = (k + lastans - 1 + MOD1) % MOD1 + 1;
      lastans = query(1, 1, 40000, k).second;
      cout << lastans << endl;
    } else {
      int a, b, x, y;
      cin >> a >> b >> x >> y;
      a = (a + lastans - 1 + MOD1) % MOD1 + 1;
      b = (b + lastans - 1 + MOD2) % MOD2 + 1;
      x = (x + lastans - 1 + MOD1) % MOD1 + 1;
      y = (y + lastans - 1 + MOD2) % MOD2 + 1;
      if (a > x) {
        swap(a, x);
        swap(b, y);
      }
      line t;
      if (a == x) {  // 垂直于 y 的函数的特殊处理
        t.k = 0;
        t.b = max(b, y);
      } else {
        t.k = (double)(y - b) / (x - a);
        t.b = b - t.k * a;
      }
      t.l = a;
      t.r = x;
      t.id = ++segi;
      modify(1, 1, 40000, t);
    }
  }
  return 0;
}

习题

参考资料