点分治,外国人称之为 Centroid decomposition,重心分解。
学习重心分解之前,自然要先了解重心。
下面统一用 $n$ 表示树上结点的个数。
在一棵树中,如果删除一个顶点后得到的最大子树的顶点数最少,那么这个点就是树的重心 (Centroid)。
重心的性质:
删除重心后得到的所有子树,其顶点数必然不超过 $n/2$。
证明:选取任意顶点作为起点,每次都沿着边向最大子树的方向移动,最终一定会到达某个顶点,将其删除后得到的所有子树的顶点数都不超过 $n/2$。如果这样的点存在的话,那么也就可以证明删除重心后得到的所有子树的顶点数都不超过 $n/2$。
记当前顶点为 $v$,如果顶点 $v$ 已经满足上述条件则停止。否则,与顶点 $v$ 邻接的某个子树的顶点数必然大于 $n/2$。假设顶点 $v$ 与该子树中的顶点 $w$ 邻接,那么我们就把顶点 $w$ 作为新的顶点 $v$。不断重复这一步骤,必然会在有限步停止。这是因为对于移动中所用的边 $(v, w)$,必有 $v$ 侧的子树的顶点数小于 $n/2$,$w$ 侧的子树的顶点数大于 $n/2$,所以不可能再从 $w$ 移动到 $v$。因而该操作永远不会回到已经经过的顶点,而顶点数又是有限的,所以算法必然在有限步终止。
树中所有顶点到某个顶点的距离和中,到重心的距离和是最小的;如果有两个重心,那么到它们的距离和一样。
把两棵树通过一条边相连得到一棵新的树,那么新的树的重心在连接原来两棵树的重心的路径上。
在一棵树上添加或删除一个叶子,那么它的重心最多只移动一条边的距离。
更多证明请见:树的重心的性质及其证明 - suxxsfe - 博客园 (cnblogs.com)
根据重心的定义,先以 $1$ 为根进行 DFS。在递归中计算子树大小 $siz[u]$,并求出最大的子树的大小 $maxs[u]$,比较出重心 $centroid$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void getCentroid ( int u , int fa , int s ) {
siz [ u ] = 1 ;
maxs [ u ] = 0 ;
for ( int i = head [ u ]; i != 0 ; i = nxt [ i ]) {
if ( to [ i ] == fa )
continue ;
getCentroid ( to [ i ], u , s );
siz [ u ] += siz [ to [ i ]];
maxs [ u ] = max ( maxs [ u ], siz [ to [ i ]]);
}
// “向上” 的部分也是该结点的子树
maxs [ u ] = max ( maxs [ u ], s - siz [ u ]);
if ( maxs [ u ] < maxs [ centroid ] || ! centroid ) centroid = u ;
}
int main () {
centroid = 0 ;
getCentroid ( 1 , 0 , n );
return 0 ;
}
提交:CSES - Finding a Centroid
我们可以用点分治解决关于统计树上路径的问题。
Luogu P3806【模板】点分治 1 :给定一棵有 $n$ 个点的带边权树,$m$ 次询问,每次询问给出 $k$,询问树上距离为 $k$ 的点对是否存在。
$n\le 10000,m\le 100,k\le 10000000$
暴力的做法至少需要 $O(n^{2})$,显然会超时,所以考虑分治。
如何分割呢?如果随意选择顶点的话,递归的深度可能退化成 $O(n)$。若我们每次选择子树的重心 作为新的根结点,可以让递归的层数最少。因为每次树的大小至少减半,所以递归的深度是 $O(log n)$。
设当前的根结点是 $rt$。
对于每一条路径 $(u, v)$,必然满足以下三种情况之一:
顶点 $u, v$ 在 $rt$ 的同一子树内。 顶点 $u, v$ 分别在 $rt$ 的不同子树内。 顶点 $u, v$ 其中一个是 $rt$。 对于第 (1) 种情况,可以递归后转化成另外的情况。对于第 (2) 种情况,从顶点 $u$ 到顶点 $v$ 的路径必然经过根结点 $rt$,只要求出每个顶点到 $rt$ 的距离,就可以统计出答案。对于第 (3) 种情况,可以添加一个到 $rt$ 距离为 $0$ 的顶点,就转化为了第 (2) 种情况。
需要注意的是,在第 (1) 种情况中统计的同一子树的顶点对,要避免在第 (2) 种情况中被重复统计。通过容斥 和类似于树上背包 的方法可以去重。
最后的时间复杂度是 $O(nlog^{2}n)$。
RECORD 。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
int n , m ;
int L , p ;
int centroid ;
bool vis [ MAXN ], cnt [ MAXW ], ans [ MAXM ];
int ask [ MAXM ];
vector < std :: pair < int , int > > g [ MAXN ];
int dis [ MAXN ];
int siz [ MAXN ], maxs [ MAXN ];
void getCentroid ( int u , int fa , int s ) {
siz [ u ] = 1 ;
maxs [ u ] = 0 ;
for ( auto i : g [ u ]) {
if ( i . first == fa || vis [ i . first ]) continue ;
getCentroid ( i . first , u , s );
siz [ u ] += siz [ i . first ];
maxs [ u ] = std :: max ( maxs [ u ], siz [ i . first ]);
}
maxs [ u ] = std :: max ( maxs [ u ], s - siz [ u ]);
if ( maxs [ u ] < maxs [ centroid ] || ! centroid )
centroid = u ;
}
// 获取子树中所有点到重心的距离
void getDis ( int u , int fa , int d ) {
dis [ p ++ ] = d ;
for ( auto i : g [ u ]) {
if ( i . first == fa || vis [ i . first ]) continue ;
getDis ( i . first , u , d + i . second );
}
}
void calc () {
L = p = 0 ;
cnt [ 0 ] = 1 ;
// 类似于树上背包
for ( auto i : g [ centroid ]) {
if ( vis [ i . first ]) continue ;
getDis ( i . first , centroid , i . second );
// 一棵一棵子树合并,不会重复统计
for ( int i = L ; i < p ; i ++ ) {
for ( int j = 0 ; j < m ; j ++ ) {
if ( dis [ i ] > ask [ j ]) continue ;
ans [ j ] |= cnt [ ask [ j ] - dis [ i ]];
}
}
for ( int j = L ; j < p ; j ++ )
cnt [ dis [ j ]] = 1 ;
L = p ;
}
// 还原 cnt 数组
for ( int i = 0 ; i < p ; i ++ )
cnt [ dis [ i ]] = 0 ; // 不能用 memset
}
void solve ( int u , int size ) {
centroid = 0 ;
getCentroid ( u , - 1 , size );
getCentroid ( centroid , - 1 , size ); // 再求一次 siz,防止后面找重心时出错
vis [ centroid ] = true ;
calc ();
for ( auto i : g [ centroid ]) {
if ( vis [ i . first ]) continue ;
solve ( i . first , siz [ i . first ]);
}
}
int main () {
solve ( 1 , n );
for ( int i = 0 ; i < m ; i ++ ) {
if ( ans [ i ]) cout << "AYE \n " ;
else cout << "NAY \n " ;
}
return 0 ;
}
需要注意的细节 :
分治的时候求出新的重心之后,也要再次 求子树 $siz$。
详见:一种基于错误的寻找重心方法的点分治的复杂度分析 - 博客 - liu_cheng_ao的博客 (uoj.ac)
账号 920848348 评论:
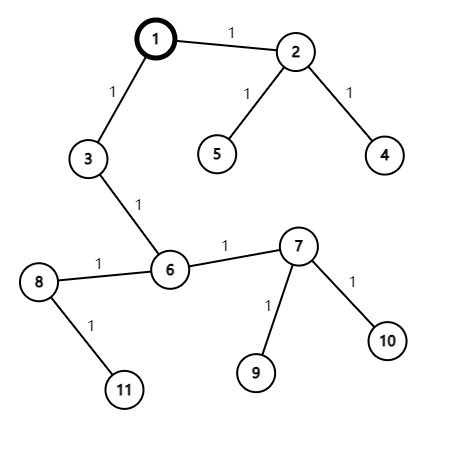
对于大部分点分治的代码中,不能直接 size = siz[v],否则会导致后面的重心求错(可以用下面的样例试一下,然后输出重心节点看一下,你会发现从 $6$->$3$ 这一大块的重心应该是 $2$,而代码输出是 $1$。原因在于:
由于一开始从 点 $1$ 开始找整棵树的重心,此时的 $siz[u]$ 表示的仅仅是以 1 为根结点的树中,$u$ 的子树大小。那么现在重心 $root$ 找到了,那么从这整棵树的重心 $root$ 开始深搜时,若有边 $root$->$v$ ,而此时的 $siz[v]$ 的值并不是以 $v$ 为根的子树的大小(这个子树当然不包括父亲 $root$ 那一块)。具体为什么,这里给一组样例,大家可以在图中画一下。
此样例的对应题目为 Luogu P3806【模板】点分治 1 。
然后我们一步一步来:
先从 $1$ 开始 dfs ,统计 $siz$ 数组,此时很清晰的知道 $siz[3] = 7$ ,因为是以 $1$ 为根深搜的。很明显,一开始这整棵树的重心是 6 号节点,那么接下来,我们可以发现:
当从点 $6$ 开始 dfs 时,有 $6$->$3$ 这条边,那么按理来说,$size = siz[3]$,此时 $size$ 表示的是以 $3$ 为根的子树的大小,可看图上明明是 $5$ 啊(在点 $3$ 的左边,不包含点 $6$ 那边)。可是此时的 $siz[3]$ 为 $7$,而并非是 $5$ 。这是由于选定的深搜节点不同,统计的不同而导致的。$siz[3]$ 的正确值理应来自于从 点 $6$ 开始深搜的值。
故我们可以得出结论,用 getroot(1,0) 找到整棵树的重心之后,再来一次 getroot(root, 0),来确定以重心为根结点时的 $siz$ 数组。这下就可以直接 size = siz[v] 了。
11 1
6 7 1
6 8 1
7 9 1
7 10 1
8 11 1
1 2 1
1 3 1
2 4 1
2 5 1
3 6 1
2
不要用 memset 粗暴还原,会浪费很多时间。
Luogu P4178 Tree :给定一棵有 $n$ 个点的带权树,给出 $k$,询问树上距离小于等于 $k$ 的点对数量。
$n\le 40000,k\le 20000,w_i\le 1000$
这题方法比较多。下面的代码用 容斥 进行去重和 双指针 (除此之外还可以用二分 )统计答案。
RECORD 。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
int calc ( int u , int w ) {
dis . clear ();
getDis ( u , - 1 , w );
sort ( dis . begin (), dis . end ());
int sum = 0 ;
int L = 0 , R = dis . size () - 1 ; // 双指针
while ( L < R ) {
if ( dis [ L ] + dis [ R ] <= k )
sum += R - L , L ++ ;
else
R -- ;
}
return sum ;
}
void solve ( int u , int size ) {
centroid = 0 ;
getCentroid ( u , - 1 , size );
getCentroid ( centroid , - 1 , size );
vis [ centroid ] = true ;
ans += calc ( centroid , 0 );
for ( auto i : g [ centroid ]) {
if ( vis [ i . first ]) continue ;
ans -= calc ( i . first , i . second ); // 容斥。去除错误的答案。
}
for ( auto i : g [ centroid ]) {
if ( vis [ i . first ]) continue ;
solve ( i . first , siz [ i . first ]);
}
}
暂且咕咕咕。🕊
Luogu P4149 [IOI2011]Race :给定一棵有 $n$ 个点的带权树,给出 $k$,求一条简单路径。权值和等于 $k$,且边的数量最小。
$n\le 200000,k,w_i\le 1000000$
开个桶数组记录最小边数即可。
RECORD 。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
// 桶数组,minn[i] 表示权值和为 i 的路径的最小边数
int minn [ MAXK ];
// d 表示权值和,b 表示边数
void getDis ( int u , int fa , int d , int b ) {
if ( d > k ) return ;
dis . emplace_back ( d , b );
for ( auto i : g [ u ]) {
if ( i . first == fa || vis [ i . first ]) continue ;
getDis ( i . first , u , d + i . second , b + 1 );
}
}
void calc ( int u ) {
minn [ 0 ] = 0 ;
tdis . clear ();
for ( auto i : g [ u ]) {
if ( vis [ i . first ]) continue ;
dis . clear ();
getDis ( i . first , u , i . second , 1 );
for ( auto j : dis ) {
if ( minn [ k - j . first ] != - 1 ) { // 可以拼凑成权值和为 k 的路径
if ( ans == - 1 )
ans = minn [ k - j . first ] + j . second ;
else
ans = std :: min ( ans , minn [ k - j . first ] + j . second );
}
}
// 更新桶数组
for ( auto j : dis ) {
tdis . push_back ( j );
if ( minn [ j . first ] == - 1 )
minn [ j . first ] = j . second ;
else
minn [ j . first ] = std :: min ( minn [ j . first ], j . second );
}
}
// 还原 minn 数组
for ( auto i : tdis ) {
minn [ i . first ] = - 1 ;
}
}
void solve ( int u , int size ) {
centroid = 0 ;
getCentroid ( u , - 1 , size );
getCentroid ( centroid , - 1 , size );
vis [ centroid ] = true ;
calc ( centroid );
for ( auto i : g [ centroid ]) {
if ( vis [ i . first ]) continue ;
solve ( i . first , siz [ i . first ]);
}
}
🙇