树状数组笔记

By Zirnc

August 15, 2022

2 minutes

早就学习过线段树了，但惭愧的是更简单的树状数组却一直没有深入理解过，仅仅停留在背代码的层级。今天认真学习一下树状数组。

引入

树状数组（Binary Index Tree, BIT / Fenwick Tree）支持单点修改和区间查询两种简单操作，时间复杂度均为 $O(\log n)$。它的实现比线段树简单，速度更快，但功能稍逊一筹。

原理

bit

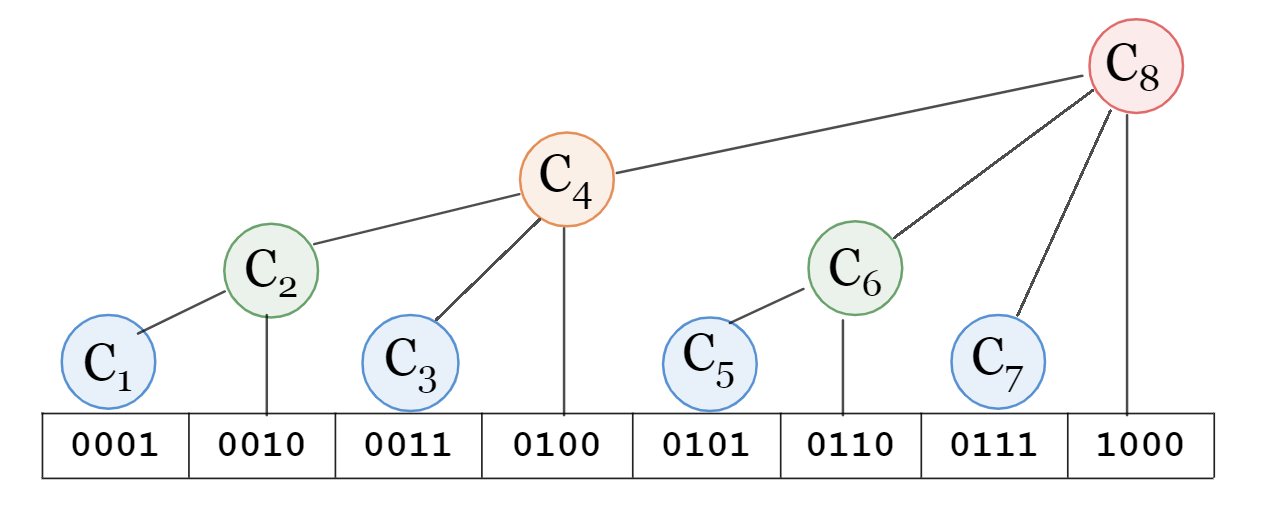
我们用 $C_i$ 来表示 $A$ 数组的一段区间，定义 $x$ 的二进制表示中，最低位的 $1$ 的位置为 $\operatorname{lowbit}(x)$，那么用 $C_i$ 代表 $A$ 数组的下标区间 $[i-\operatorname{lowbit}(i)+1, i]$。举个例子，$4_{(10)} = 100_{(2)}$，$100_{(2)}-\operatorname{lowbit}(100_{(2)})+1_{(2)}=1_{(2)}=1_{(10)}$，那么 $C_4$ 代表的区间就是 $[1, 4]$。通过这样的设计，树状数组将结点数压缩到与数组长度相同，不像线段树一样需要 $2n$ 个结点。

之所以会有这个特点，是因为对于位置 $i$，其对应的结点所在的高度就是 $\operatorname{lowbit}(i)$ 的位数。第一层结点为全体 $2^0 + 2^1k$，即所有 $\operatorname{lowbit}(i)=1$ 的数字；第二层结点为全体 $2^1 + 2^2k$ ，即所有 $\operatorname{lowbit}(i)=2$ 的数字；第三层结点为全体 $2^2 + 2^3k$ ，即所有 $\operatorname{lowbit}(i)=4$ 的数字；以此类推。也就是说，对于位置 $i$，在这个位置往上垂直追溯，能追溯的层数就是 $i$ 的二进制表示的末尾 $0$ 数量。而结点高度又决定了其子树的大小，于是它所代表的信息区间大小也就一定是 $2^{i的末尾0数量}=\operatorname{lowbit}(i)$。
*来源于参考资料 1

实现

$\operatorname{lowbit}$ 如何计算呢？我们有这样一条公式：$\operatorname{lowbit}(x)=(x)&(-x)$。在计算机中，有符号数采用补码表示。在补码表示下，$x$ 的相反数 -x = ~x + 1，也就是按位非再加一。例如 $x$ 的最后一个 $1$ 的位置附近是 $\cdots 01000\cdots$，按位非之后是 $\cdots 10111\cdots$，加一再变成 $\cdots 11000\cdots$；而前面每一位都与原来相反。这时我们再把它和 $x$ 按位与，得到的结果为 $01000\cdots$ 即 $\operatorname{lowbit}(x)$。

单点修改

修改操作类似于向上爬树的过程。例如我们要修改第三个元素，那么依次要修改 $C_3, C_4, C_8$，用二进制表示就是 $11, 100, 1000$，发现下标 $x$ 每次都要 $x += \operatorname{lowbit}(x)$，直到到达顶部。

1
2
3
4
5
6
int add(int x, int y) {
	while (x <= n) {
		tree[x] += y;
		x += lowbit(x);
	}
}

区间查询（前缀和）

例如查询第六个元素的前缀和，即 $[1, 6]$ 这一区间。首先 $C_6$ 表示的区间是 $[5, 6]$，然后跳到 $C_4$，代表的区间是 $[1, 4]$，加起来就 OK 了。从 $C_6$ 到 $C_4$ 是怎么跳的呢？实际上是 $110 - \operatorname{lowbit}(110) = 100$。所以下标 $x$ 每次都要 $x -= \operatorname{lowbit}(x)$，直到 $x<1$。

1
2
3
4
5
6
7
8
int query(int x) {
	int sum = 0;
	while (x) {
		sum += tree[x];
		x -= lowbit(x);
	}
	return sum;
}

至于求 $[a, b]$ 这一区间的和，只需要分别求 $[1, b]$ 和 $[1, a)$ 再相减即可。

$O(n)$ 建树

暴力的建树方法是进行 $n$ 次单点修改，时间复杂度为 $O(n\log n)$。

有两种方法可以实现 $O(n)$ 建树。

前缀和

前面讲到 $C_i$ 表示的区间是 $[i-\operatorname{lowbit}(i)+1, i]$，那么我们可以先预处理一个 $sum$ 前缀和数组，再计算 $C$ 数组。

1
2
3
4
5
void init() {
  for (int i = 1; i <= n; ++i) {
    C[i] = sum[i]-sum[i-lowbit(i)];
  }
}

倒着贡献

我们很容易知道当前点 $i$ 的父亲是 $i+\operatorname{lowbit}(i)$，所以用自己的值更新父亲即可。

1
2
3
4
5
6
7
void init() {
  for (int i = 1; i <= n; ++i) {
    C[i] += a[i];
    int j = i + lowbit(i);
    if (j <= n) C[j] += C[i];
  }
}

参考资料

斜率优化 DP 笔记

李超线段树笔记